とーとで見つけたこの問題を解いてみた

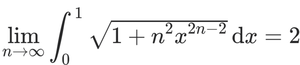
左辺が2となることを証明せよ、という問題らしい。愚直に計算してもいいが、

1+n²x^(2n-2)=1+((x^n)')²

であるため与えられた積分は、曲線y=x^nの閉区間[0,1]における長さを与える。n→∞で曲線が、原点と(1,0)を結ぶ線分および(1,0)と(1,1)を結ぶ線分に限りなく近づく、ということは直感的に想像がつくので、これを利用して解くことにする。

曲線y=x^nと、直線y=-x+1の0<x<1の部分の交点のx座標をaと置く。εを十分小さな任意の実数とし、x^N<εとなるようなNを取れば、-x+1=x^nである限り-x+1<ε。よってn→∞でaは1に収束する。ここで与えられた積分を以下のように和の形へ分解する。

∫[0,1]√(1+n²x^(2n-2))dx

=∫[0,1-a]√(1+n²x^(2n-2))dx+∫[1-a,1]√(1+n²x^(2n-2))dx

[0,1-a]において、x=1-aがx^nの最大値を与えるので、n→∞でf_n(x)=x^nは定数関数f(x)=0に一様収束する。従って

lim[n→∞]∫[0,1-a]√(1+n²x^(2n-2))dx=1

また、関数f_n(x)=x^nの逆関数f⁻¹_n(x)=x^(-n)を考えると、積分の性質から曲線y=f⁻¹_n(x)のa≤x≤1における長さは曲線y=f_n(x)のa≤x≤1の長さに等しくなることが分かる。先ほどの議論と同様に考えるとy=f⁻¹_n(x)は定数関数f(x)=1に一様収束するため、

lim[n→∞]∫[1-a,1]√(1+n²x^(2n-2))dx

=lim[n→∞]∫[1-a,1]√(1+((f⁻¹_n(x))')²)dx

=1

従って

lim[n→∞]∫[0,1]√(1+n²x^(2n-2))dx

=lim[n→∞]∫[0,1-a]√(1+n²x^(2n-2))dx+∫[1-a,1]√(1+n²x^(2n-2))dx

=1+1

=2